哈希算法揭秘：加密货币安全的基石？附SHA256计算过程

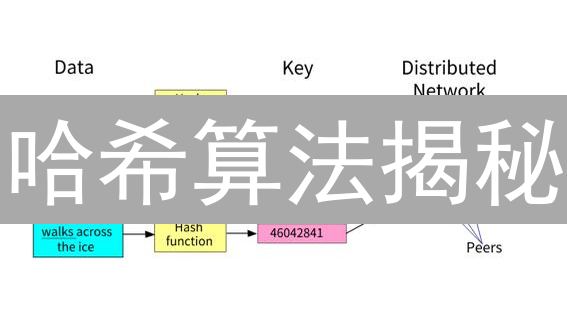
哈希值如何计算

哈希值，又称散列值，是数据经过哈希函数计算后得到的固定长度的唯一标识符。 在加密货币和区块链技术中，哈希值扮演着至关重要的角色，用于保证数据的完整性、验证交易的有效性以及创建不可篡改的区块链。 了解哈希值的计算方法对于理解加密货币的工作原理至关重要。

哈希函数的基本原理

哈希函数是密码学和计算机科学中一种至关重要的工具，它接收任意长度的数据作为输入，例如文本、图像、文件、交易记录等，并将其转换为固定长度的哈希值，也称为摘要或指纹。哈希函数的设计目标是高效地将大量数据映射到有限的哈希值空间中。一个理想的哈希函数应具备以下几个核心特性：

• 确定性（Determinism）： 这是哈希函数最基本的要求。对于相同的输入，无论何时何地进行计算，哈希函数必须始终生成完全相同的哈希值。这种确定性确保了数据的一致性和可预测性，是验证数据完整性的基础。
• 高效性（Efficiency）： 哈希函数必须能够快速地计算哈希值，以便能够及时处理大规模的数据。在实际应用中，哈希函数的计算速度直接影响系统的性能，尤其是在高吞吐量的环境中。
• 单向性（One-way property）： 单向性，也称为不可逆性，是指从哈希值反向推导出原始输入在计算上是不可行的。即使攻击者获得了哈希值，也无法通过有效的手段还原出原始数据。这种特性是哈希函数用于保护敏感信息的重要基础。单向性并非绝对，而是指在当前的计算能力下，逆向计算的成本极高，以至于不具有实际意义。
• 抗碰撞性（Collision Resistance）： 抗碰撞性是指哈希函数应尽量避免不同输入产生相同哈希值的情况，即碰撞。理想的哈希函数应使得找到两个不同的输入，产生相同哈希值的概率极低。抗碰撞性对于保证数据的唯一性和完整性至关重要，尤其是在数据存储、检索和验证等场景中。

抗碰撞性通常分为两种不同的强度：弱抗碰撞性（第一原像抵抗）和强抗碰撞性（第二原像抵抗）。

• 弱抗碰撞性 (Weak Collision Resistance / First Preimage Resistance)： 给定一个特定的输入 x 及其对应的哈希值 h(x) ，弱抗碰撞性意味着在计算上几乎不可能找到另一个不同的输入 y (其中 y != x )，使得 h(y) = h(x) 。 换句话说，攻击者难以找到一个与已知输入具有相同哈希值的其他输入。
• 强抗碰撞性 (Strong Collision Resistance / Second Preimage Resistance)： 强抗碰撞性要求在计算上几乎不可能找到任意两个不同的输入 x 和 y ，使得它们的哈希值相同，即 h(x) = h(y) 。这意味着攻击者无法主动构造出两个具有相同哈希值的输入。

强抗碰撞性比弱抗碰撞性更严格。 如果一个哈希函数具备强抗碰撞性，那么它必然也具备弱抗碰撞性。 强抗碰撞性不依赖于任何预先给定的输入，攻击者需要主动寻找任何两个碰撞的输入，因此难度更高。 在安全性要求较高的场景下，通常需要选择具备强抗碰撞性的哈希函数，以确保数据的安全性。

常见的哈希算法

加密货币领域广泛应用多种哈希算法，每种算法都有其独特的特性、优势和潜在的局限性。选择合适的哈希算法对于确保加密货币系统的安全性、完整性和效率至关重要。下面列出了一些在加密货币和区块链技术中常见的哈希算法，并对其特性进行了详细说明：

• MD5 (Message-Digest Algorithm 5): 一种曾经被广泛使用的哈希算法，能够生成 128 位的哈希值（也称为消息摘要）。尽管 MD5 曾经很流行，但现在已经被认为是不安全的。MD5 的主要问题在于它容易受到碰撞攻击。这意味着攻击者可以找到两个不同的输入，但它们会生成相同的 MD5 哈希值。由于这些安全漏洞，MD5 不再推荐用于任何安全敏感的应用，例如数字签名或数据完整性验证。
• SHA-1 (Secure Hash Algorithm 1): 类似于 MD5，SHA-1 算法生成 160 位的哈希值。在设计上，SHA-1 旨在修复 MD5 中的某些缺陷，因此最初被认为比 MD5 更安全。然而，随着时间的推移，研究人员也发现了 SHA-1 中的安全漏洞，包括碰撞攻击的可能性。虽然攻击 SHA-1 比攻击 MD5 更困难，但 SHA-1 已经不再被认为是足够安全的，并且已经被更强大的哈希算法所取代。现在，许多应用程序和协议已经停止使用 SHA-1。
• SHA-256 (Secure Hash Algorithm 256-bit): SHA-256 是 SHA-2（安全哈希算法 2）家族中最常用的哈希函数之一。顾名思义，SHA-256 生成 256 位的哈希值。比特币区块链使用 SHA-256 算法进行工作量证明（Proof-of-Work），对交易数据和区块头进行哈希处理。SHA-256 具有强大的抗碰撞能力，这意味着找到两个不同的输入，使其产生相同的 SHA-256 哈希值在计算上是极其困难的。至今，SHA-256 仍然被认为是相对安全的，并在各种安全应用中得到广泛应用，包括数据完整性验证、数字签名和密码存储。
• SHA-512 (Secure Hash Algorithm 512-bit): 另一种 SHA-2 算法，与 SHA-256 类似，SHA-512 生成 512 位的哈希值。因此，SHA-512 提供了比 SHA-256 更高的安全性，因为它产生的哈希值更大，碰撞攻击的难度更高。然而，SHA-512 的计算成本也比 SHA-256 更高，这意味着它需要更多的计算资源和时间来生成哈希值。SHA-512 通常用于需要极高安全性的应用中，例如关键数据的保护和高安全级别的密码存储。
• RIPEMD-160 (RACE Integrity Primitives Evaluation Message Digest): RIPEMD-160 是一种 160 位的哈希函数，由欧洲 RIPE（RACE Integrity Primitives Evaluation）项目开发。RIPEMD-160 是一种经过优化的哈希算法，旨在提供良好的安全性和效率。它在计算资源有限的设备上表现良好。RIPEMD-160 通常用于比特币地址的生成，具体来说，它是比特币脚本哈希地址（P2SH）的一部分。
• Keccak-256 (SHA-3): Keccak-256 是 SHA-3 标准的一部分，虽然它也生成 256 位的哈希值，但与 SHA-2 系列的算法在设计上是截然不同的。SHA-3 并不是对 SHA-2 的增强或修复，而是基于一种全新的密码学方法，称为海绵结构（Sponge Construction）。以太坊区块链使用 Keccak-256 算法，更准确地说是使用 Keccak-256 的一个变体。选择 Keccak-256 的原因在于其设计具有更高的安全边际，并且在面对未来潜在的攻击时可能更具抵抗力。

SHA-256 哈希算法的计算过程

SHA-256 是一种广泛使用的密码学哈希函数，属于 SHA-2（安全哈希算法 2）家族。 它将任意长度的输入数据转化为固定长度（256 位或 32 字节）的哈希值。 SHA-256 的设计目标是提供高安全性，使其难以通过哈希值反推出原始输入数据，也难以找到具有相同哈希值的两个不同的输入数据（抗碰撞性）。 其计算过程涉及一系列复杂的数学和逻辑运算，确保结果的唯一性和不可逆性。理解其计算过程有助于我们更好地认识加密技术的本质。

1. 填充 (Padding): 输入数据在哈希计算之前，必须进行填充，以保证其长度符合 SHA-256 算法的特定要求。 SHA-256 算法要求消息的长度是 512 位的整数倍， 因此需要进行填充。
   • 添加 "1" 比特: 在原始消息的末尾添加一个 "1" 比特。 这一步是为了明确区分原始消息和填充部分。
   • 添加 "0" 比特: 接着，添加若干个 "0" 比特，直到消息的长度（不包括最后附加的长度信息）比 512 的倍数小 64 位。 也就是说，填充后的消息长度模 512 应该等于 448。
   • 附加长度信息: 将原始消息的长度（以比特为单位）表示为一个 64 位的无符号整数，并将其附加到填充后的消息末尾。 这确保了即使原始消息不同但填充后的消息长度相同，最终的哈希值也会不同。 64 位足以表示长度不超过 2^64 比特的消息。
2. 解析 (Parsing): 完成填充后，消息被分割成 512 位的块，也称为消息块。 每个块将独立地进行处理。 SHA-256 算法的核心是对这些 512 位的块进行迭代处理。 将数据分成固定大小的块，方便进行后续的计算操作。
3. 初始化哈希值 (Initialization of Hash Values): SHA-256 算法使用 8 个 32 位的哈希值（也称为链接变量）来维护计算的中间状态。 这些哈希值在算法开始时被初始化为预定义的常量。 这些常量基于自然数前 8 个质数（2, 3, 5, 7, 11, 13, 17, 19）的平方根的小数部分的前 32 位，提高了算法的安全性。 这些初始哈希值会在每一轮的压缩函数中被更新，最终生成最终的哈希值。
4. 处理块 (Process Blocks): 这是 SHA-256 算法的核心部分，它对每个 512 位的消息块进行处理。 处理过程包括消息调度和压缩函数两个关键步骤。
   • 消息调度 (Message Schedule): 将 512 位的消息块扩展成 64 个 32 位的字（words），记为 W0, W1, …, W63。 前 16 个字 (W0 到 W15) 直接取自消息块。 剩余的字 (W16 到 W63) 通过一个复杂的计算过程生成， 这个过程涉及到前几个字的位运算和逻辑运算。 消息调度确保每个消息位的变化都会影响到后续的计算，提高了算法的雪崩效应。 具体计算公式如下：
     W _i =
     σ ₁ (W _i-2 ) + W _i-7 + σ ₀ (W _i-15 ) + W _i-16
     其中 σ ₀ (x) 和 σ ₁ (x) 是两个非线性函数，定义为：
     σ ₀ (x) = ROTR ⁷ (x) ⊕ ROTR ¹⁸ (x) ⊕ SHR ³ (x)
     σ ₁ (x) = ROTR ¹⁷ (x) ⊕ ROTR ¹⁹ (x) ⊕ SHR ¹⁰ (x)
     其中 ROTR ⁿ (x) 表示将 x 循环右移 n 位，SHR ⁿ (x) 表示将 x 右移 n 位（丢弃右边的 n 位，左边补 0）。
   • 压缩函数 (Compression Function): 压缩函数是 SHA-256 算法的核心组件，它接受当前的 8 个哈希值（H0 到 H7）以及 64 个消息字（W0 到 W63）作为输入，并通过 64 轮的迭代计算来更新哈希值。 每轮计算都包括一系列的位运算（如 XOR, AND, NOT）、模加运算和循环移位操作。 每一轮还使用一个预定义的常量 K _i ， 这些常量基于自然数前 64 个质数的立方根的小数部分的前 32 位。 压缩函数的每一轮计算都旨在混合和扩散输入数据，使得输出对输入的微小变化非常敏感。 在每一轮计算中，哈希值会被更新，具体过程涉及到多个中间变量和复杂的计算步骤。详细的计算过程可以参考 SHA-256 的标准文档。
5. 输出 (Output): 经过所有消息块的处理后，最终的 8 个哈希值（H0 到 H7）被连接起来，形成 256 位的哈希值， 这个哈希值就是 SHA-256 算法的输出。 这个输出是输入数据的“指纹”，具有唯一性和不可逆性。

SHA-256 算法的实现相当复杂，涉及到大量的位运算和逻辑运算。 由于其复杂性和安全性要求，通常使用专门的软件库（如 OpenSSL）或硬件加速器来实现。 手动计算 SHA-256 哈希值几乎是不可能的，尤其对于较大的输入数据。 现代编程语言和安全框架通常都提供了 SHA-256 的内置支持，方便开发者使用。

哈希值在加密货币中的应用

哈希值是加密货币和区块链技术的核心组成部分，在保障数据安全和实现去中心化方面发挥着至关重要的作用。它们在各种场景中被广泛应用，以下是一些常见的例子，并对其原理和重要性进行更详细的阐述：

• 交易哈希： 每当一笔新的交易发生时，这笔交易的全部信息（包括发送方地址、接收方地址、交易金额、手续费等）都会经过哈希函数的处理，生成一个唯一的交易哈希值（Transaction Hash）。这个哈希值就像是这笔交易的“指纹”，具有唯一性和不可篡改性。它不仅用于在区块链网络中唯一标识这笔交易，方便追踪交易状态，而且还作为交易数据完整性的重要保障，确保交易内容不被恶意篡改。交易哈希也被包含在区块中，为后续的验证和查询提供依据。
• 区块哈希： 区块链由一个个区块链接而成，每个区块都包含一定数量的交易记录。每个区块的头部（Block Header）包含多个关键信息，包括前一个区块的哈希值（Previous Block Hash）、时间戳（Timestamp）、用于证明工作量的信息（Nonce）、以及默克尔树根（Merkle Root）等。将这些信息通过哈希函数处理，就能生成当前区块的唯一区块哈希值（Block Hash）。区块哈希值的作用至关重要，它不仅唯一标识了当前区块，而且通过包含前一个区块的哈希值，将所有区块按照时间顺序链接在一起，形成不可篡改的链式结构，保证了区块链数据的完整性和连续性。
• 工作量证明 (Proof-of-Work): 在采用工作量证明机制（PoW）的加密货币中，例如比特币，矿工需要通过不断尝试不同的随机数（Nonce）来计算区块哈希值。矿工的目标是找到一个满足特定难度要求的区块哈希值，这个难度通常由目标值（Target）来表示。 只有当计算出的区块哈希值小于或等于目标值时，该区块才被认为是有效的，矿工才能获得奖励。 工作量证明的过程需要消耗大量的计算资源，从而增加了攻击者篡改区块链数据的成本，有效地防止了双重支付攻击和其他恶意行为。这种机制确保了区块链网络的安全性和可靠性。
• 默克尔树 (Merkle Tree): 默克尔树是一种用于高效验证大规模数据完整性的树形数据结构。在区块链中，每个区块包含大量的交易记录，如果直接对所有交易记录进行哈希处理，效率会非常低下。因此，区块链采用默克尔树结构，首先将每笔交易的哈希值作为叶子节点，然后将相邻的两个叶子节点的哈希值进行哈希运算，生成它们的父节点，以此类推，直到最终生成一个根节点，这个根节点被称为默克尔根哈希值（Merkle Root）。默克尔根哈希值包含了区块中所有交易信息的摘要，并被包含在区块头中。 通过默克尔树，可以快速验证区块中某个特定交易是否存在以及是否被篡改，而无需下载整个区块的数据，极大地提高了验证效率。
• 地址生成： 许多加密货币使用哈希函数来从公钥派生出钱包地址。例如，比特币使用 SHA-256 和 RIPEMD-160 算法对公钥进行两次哈希处理，然后进行Base58Check编码，生成最终的比特币地址。 这种方法可以缩短地址长度，提高可读性，并增加地址的安全性。 通过哈希函数生成地址，可以有效地保护用户的隐私，防止公钥直接暴露在区块链网络中。

哈希值在加密货币领域扮演着至关重要的角色。 从交易验证到区块链接，从工作量证明到地址生成，哈希函数被广泛应用于各个环节，确保了加密货币系统的安全性、透明性和可靠性。 它们是构建安全可靠的区块链系统的基石，为数字经济的发展提供了坚实的技术保障。